Unit 4 test triangle congruence – Embark on a captivating journey into the realm of Unit 4: Triangle Congruence. This fundamental concept holds the power to unlock a world of geometric mysteries and practical applications. Dive into the intricacies of the SSS, SAS, ASA, and AAS theorems, and witness how they empower you to prove triangles congruent with precision and confidence.

Beyond the theoretical realm, discover the practical significance of triangle congruence in architecture, engineering, and design. Learn how it guides the construction of stable structures, enables accurate measurements, and inspires artistic creations. Prepare to be amazed by the elegance and versatility of this geometric principle.

Triangle Congruence Theorems

Triangle congruence theorems provide criteria to determine whether two triangles are congruent, meaning they have the same size and shape. These theorems are essential in geometry for proving the equality of triangles and solving various geometric problems.

Side-Side-Side (SSS) Congruence Theorem

The SSS Congruence Theorem states that if the three sides of one triangle are equal to the three sides of another triangle, then the triangles are congruent. This means that the triangles have the same shape and size.

SSS Congruence Theorem:If \(a = a’, b = b’,\) and \(c = c’\), then \(\triangle ABC \cong \triangle A’B’C’\).

Side-Angle-Side (SAS) Congruence Theorem

The SAS Congruence Theorem states that if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent. This theorem is particularly useful when one side and two angles of a triangle are known.

SAS Congruence Theorem:If \(a = a’, b = b’,\) and \(\angle C = \angle C’\), then \(\triangle ABC \cong \triangle A’B’C’\).

Example:

Given a triangle with sides \(a = 5 cm\), \(b = 7 cm\), and \(c = 9 cm\), and another triangle with sides \(a’ = 5 cm\), \(b’ = 7 cm\), and \(c’ = 9 cm\), we can conclude that the triangles are congruent by the SSS Congruence Theorem.

Proving Triangle Congruence

Proving triangle congruence involves demonstrating that two triangles are identical in shape and size. This can be achieved using various congruence theorems, each with its own specific conditions and method of proof.

SSS Congruence Theorem

The SSS (Side-Side-Side) Congruence Theorem states that if the three sides of one triangle are equal to the three sides of another triangle, then the triangles are congruent.

Proof:

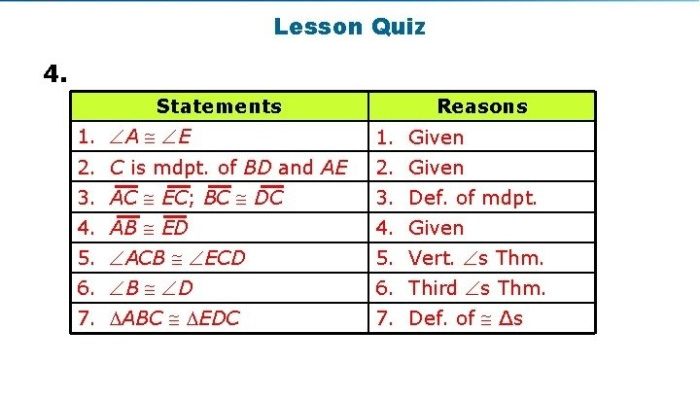
1. Given: ΔABC ≅ ΔXYZ with AB = XY, BC = YZ, and AC = XZ.
2. By the definition of triangle congruence, ΔABC and ΔXYZ have the same shape and size.
3. Therefore, ΔABC ≅ ΔXYZ.

SAS Congruence Theorem

The SAS (Side-Angle-Side) Congruence Theorem states that if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.

Proof:

1. Given: ΔABC ≅ ΔXYZ with AB = XY, BC = YZ, and ∠B = ∠Y.
2. By the definition of triangle congruence, ΔABC and ΔXYZ have the same shape and size.
3. Therefore, ΔABC ≅ ΔXYZ.

ASA Congruence Theorem

The ASA (Angle-Side-Angle) Congruence Theorem states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.

Proof:

1. Given: ΔABC ≅ ΔXYZ with ∠A = ∠X, ∠B = ∠Y, and AB = XY.
2. By the definition of triangle congruence, ΔABC and ΔXYZ have the same shape and size.
3. Therefore, ΔABC ≅ ΔXYZ.

AAS Congruence Theorem

The AAS (Angle-Angle-Side) Congruence Theorem states that if two angles and a non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.

Proof:

1. Given: ΔABC ≅ ΔXYZ with ∠A = ∠X, ∠B = ∠Y, and AC = XZ.
2. By the definition of triangle congruence, ΔABC and ΔXYZ have the same shape and size.
3. Therefore, ΔABC ≅ ΔXYZ.

Table of Congruence Theorems

The following table summarizes the four triangle congruence theorems, highlighting their similarities and differences:

Theorem	Conditions	Proof Method
SSS	Three sides equal	By definition
SAS	Two sides and included angle equal	By definition
ASA	Two angles and included side equal	By definition
AAS	Two angles and non-included side equal	By definition

Applications of Triangle Congruence

Triangle congruence is a fundamental concept in geometry that finds numerous applications in architecture, engineering, design, and geometric constructions and transformations. It is also essential in solving geometric puzzles and problems.

Architecture, Unit 4 test triangle congruence

• Ensuring the stability and symmetry of buildings by making sure corresponding triangles in the structure are congruent.
• Creating aesthetically pleasing designs by utilizing congruent triangles to achieve balance and harmony.

Engineering

• Designing bridges and other structures that require precise measurements and congruent components to ensure stability and load-bearing capacity.
• Creating machines and mechanisms that rely on congruent parts to function smoothly and efficiently.

Design

• Creating visually appealing logos, patterns, and artwork by using congruent triangles to establish symmetry and cohesion.
• Designing furniture and other objects with congruent parts to achieve aesthetic appeal and functionality.

Geometric Constructions and Transformations

Triangle congruence plays a crucial role in geometric constructions, such as:

• Constructing congruent triangles using different methods, such as the side-side-side (SSS), side-angle-side (SAS), and angle-side-angle (ASA) congruence theorems.
• Performing transformations on triangles, such as rotations, translations, and reflections, while maintaining triangle congruence.

Solving Geometric Puzzles and Problems

Triangle congruence is essential for solving various geometric puzzles and problems, including:

• Determining whether two triangles are congruent based on given information about their sides and angles.
• Solving problems involving angle bisectors, perpendicular bisectors, and medians of triangles using triangle congruence.
• Using triangle congruence to prove other geometric properties, such as the Pythagorean theorem.

Triangle Congruence and Transformations: Unit 4 Test Triangle Congruence

Triangle congruence is closely related to geometric transformations, such as rotations, reflections, and translations. These transformations can be used to prove triangle congruence and to create congruent triangles.

Rotations

A rotation is a transformation that turns a figure around a fixed point. When a triangle is rotated, its shape and size remain the same. Therefore, if two triangles are congruent, they can be rotated to be in the same orientation.

Reflections

A reflection is a transformation that flips a figure over a line. When a triangle is reflected, its shape and size remain the same, but its orientation changes. Therefore, if two triangles are congruent, they can be reflected over the same line to be in the same orientation.

Translations

A translation is a transformation that moves a figure from one point to another. When a triangle is translated, its shape and size remain the same, and its orientation does not change. Therefore, if two triangles are congruent, they can be translated to be in the same position.

Diagram Illustrating the Relationship between Triangle Congruence and Transformations

The following diagram illustrates the relationship between triangle congruence and transformations:

In the diagram, the triangle on the left is congruent to the triangle on the right. The triangle on the left has been rotated 90 degrees to create the triangle on the right. The triangle on the right has been reflected over the line y = x to create the triangle on the left. The triangle on the left has been translated 5 units to the right to create the triangle on the right.

FAQ Resource

What is the most fundamental triangle congruence theorem?

The Side-Side-Side (SSS) Congruence Theorem, which states that if two sides and the included angle of one triangle are congruent to the corresponding sides and included angle of another triangle, then the triangles are congruent.

How can I prove triangle congruence using the AAS theorem?

If two angles and a non-included side of one triangle are congruent to the corresponding angles and non-included side of another triangle, then the triangles are congruent.

What is the practical significance of triangle congruence in architecture?

Triangle congruence ensures the stability of structures by guaranteeing that corresponding sides and angles of load-bearing elements are equal, distributing weight evenly and preventing collapse.